Forum Replies Created
-
Posts
-
Hi Caldreas, welcome to the forum! Sorry for the late response, we all live in the New Orleans area and we just got hit by a major hurricane. Power was out at my house for 9 days. So I’m just getting back online.
Glad you are having fun testing the system out, and would love to hear more about it. If you have any specific questions on the rules, don’t be shy to ask.
Yeah, I don’t know – I think I’ve probably dropped a sword maybe 1 out of 6 practices at some point, (with each practice typically on a Sunday, I don’t know 3 to 5 matches with ~10 bouts each, so 30-50 bouts?) but I’d attribute even that to a generally lackadaisical or relaxed atmosphere during routine training / free play. As in literally holding the sword looser so as to more easily ‘pull’ a blow if I strike someone. I’ve been in I think about 15 tournaments and I never dropped a sword in any of those matches. Which I’d attribute to taking the whole thing a bit more seriously. So I think 1 in 20 chance of a serious fumble is really exaggerated, personally.
Maybe a partial stumble or something, I could see one out of twenty, but falling over, as in landing on the ground? I don’t think that happens often, unless we are doing grappling or demonstrating a disarm or something. Once a year or every other year maybe, if that? I can’t say I remember you actually falling down at practice before? I think I have once or twice in the last several years.
Master of the housbook is also called ‘Master of the Amsterdam Cabinet’ – he’s anonymous, nobody knows his true identity. Look at this magnificent Turk he did:
So bottom line, 3d6 is “less swingy” than one d20, though I guess it depends what you mean by that term.
Hey sorry Zarlor I was working on my reply before your post showed up.
So here is how I see it. What his saying is that 3d6 will have the same average as 1d18. Which is technically true. In both cases your average is going to be about 9 or 10 or whatever. But what matters most for players from my experience is not being flogged with the flat curve. They want to avoid the negative outiliers. So with 3d6, they want to avoid rolling a 3. And 3d6 would be better for this than say, determining a number between 3-18 via percentile dice or something.
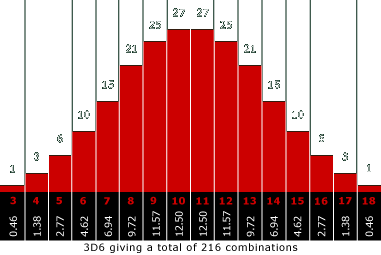
I’ll post some hard numbers on this later when I have time to do a bit more coding, (and I’m sure you know this already but bear with me as I restate the obvious), but basically a bell curve result such as you get from 3d6 means that most of the die roll results you are going to get are going to be in the middle range, 8-13. If you add up the number of results you get from rolling 3d6 10,000 times, something like 2/3 will be in that middle range, while the higher and lower results will be about 1/3. The chart above matches that ratio I think.
This gives you the experience of having far fewer outlier results. The curve skews toward the middle.
With the ‘advantage’ system as you call it (though I am loath to do so!) the curve skews more and more toward the top, and increasingly diminishes the chances of a ‘critical failure’ That is what matters most in my experience especially for your more tightly wound or angry players (like one or two people in your group): NOT getting a critical fail. The baseline with a 20 sided die is about 20% chance (around 4% in my test but that is because I used a small sample, it evens out the more iterations you do).
Rolling two dice reduces that critical fail chance already to about 2.5%, which helps (that is half of the normal risk), but 3 dice reduces it to 1%, a big improvement (a fifth of the normal risk). At four dice the chances are one quarter of one percent. This allows those players who can’t stand to get a Crit Fail to really avoid them if they are willing to spend the dice (or manage to min-max the situation to arrange for enough extras). The average die roll also goes up, but kind of gradually, as does the chance of a crit success, but still not to the point that it becomes routine (it becomes around a 1 in 8 chance based on my last test, though I think it ends up being about 1 in 6 or 7).
So this is what solves my problem. Skewing the numbers higher, as an option which players ‘pay’ for in one way or another. Some people like to gamble, and don’t mind the flat curve. Others can never get used to it, they feel like something is wrong and I’d say there is. Your chance of dropping a sword really isn’t one in twenty if you are paying attention to what you are doing. Especially if you are experienced. That’s why it feels off.
Ok … after thinking that over a bit more, I think I DO get what that guy was trying to say, but I don’t think it’s relevant. I’ll explain why in a minute.
Here are the results of my first test. For this first run I’m only doing 2000 rolls at a time because my program is pretty crude and it runs slow, I’ll fine tune it a bit later. Messing around with this already forced me to address a nagging rounding error on my random number generator for the character lifepath application, so that’s a positive side benefit even though it took me 3 hours to fix it + write this number cruncher thing.
So ok anyway, this is a ‘Monte Carlos’ test of Roll many / Keep one, keeping the highest number of dice rolled out of one, two, three, and four. I’m tracking the number of Critical Failure and Critical Success results which are key for reasons I’ll explain in a followup post.
Anyway, here are preliminary results.
Roll ONE die
Number of Natural 20: 76 (3.8%)
Number of Natural 1: 83 (4.1%)
Iterations: 2000
Cumulative total: 20786
Average: 10.39Roll TWO dice
Number of Natural 20: 125 (6.2%)
Number of Natural 1: 52 (2.6%)
Iterations: 2000
Cumulative total: 23333
Average: 11.67Roll THREE dice
Number of Natural 20: 206 (10.3%)
Number of Natural 1: 18 (0.9%)
Iterations: 2000
Cumulative total: 26539
Average: 13.27Roll FOUR dice
Number of Natural 20: 241 (12.05%)
Number of Natural 1: 5 (0.25%)
Iterations: 2000
Cumulative total: 28063
Average: 14.03“Yes, 3d6 are less “swingy” than a straight percentile in the roll, but the roll is not the relevant part, it’s the outcome you are concerned with, after all.”
This is the part I don’t get, I don’t understand this distinction. I’m writing the program to do the ‘Casino’ test now.
Ah, I thought that is what they are saying, and thanks for explaining it… but I don’t agree! I think you get much more ‘middle’ numbers with an ordinary bell curve (i.e., 3d6 vs. 1d18) and you’ll skew much higher AND almost never roll a ‘natural 1’ if you pick the highest out of multiple dice. Maybe it’s time to run another ‘Monte Carlos’ simulation on my computer to make the point.
